Blog

Planparalel

Fisika
Plan parallel adalah benda bening yang di batasi dua bidang datar yang sejajar.
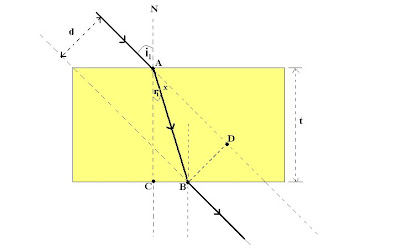
Keunikan Plan Parallel terletak pada kemampuannya menggeser sinar (d).


Keterangan gambar.

d = pergeseran sinar;t=tebal plan parallel;N=garis normal; i1 = sudut datang bidang bias pertama; r1 = sudut bias bidang bias pertama

Bagaimana cara menemukan rumus pergeseran sinar (d) ?

Perhatikanlah !!!

1.Amatilah segitiga ABC!
Sudut ACB = 90 derajat, karena merupakan garis normal. Jadi sisi AB nya sebagai sisi miring.

AC/AB = cos r1
AB = AC/cos r1 ………( Persamaan 1)

2. Amatilah segitiga ABD!
Sudut ADB = 90 derajat , Jadi sisi AB nya sebagai sisi miring juga.

DB/AB = sin X
AB = DB/sin X ………( Persamaan 2)

3.Amatilah titik A !

Sudut i1 = r1 + X ( karena sudut bertolak belakang)

X = i1 – r1 …..(Persamaan 3)

4. Amatilah gambar keseluruhan!
Ternyata AC = t ( tebal plan pararel)
DB = d ( pergeseran sinar)

5. Dari persamaan 1, 2 dan 3 dapat diturunkan sebagai berikut:

DB/sin X = AC/cos r1
d/sin (i1-r1)= t/cos r1

d = {t.sin (i1-r1)}/cos r1

Prisma

Fisika
Prisma: adalah benda bening yang dibatasi dua bidang datar yang membentuk sudut.

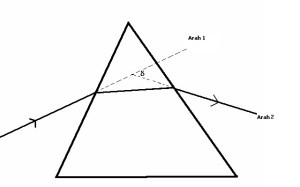
Keunikan Prisma adalah dapat menyimpangkan arah berkas cahaya. Penyimpangan arah tersebut dinamakan sudut deviasi (δ)

Keterangan Gambar:
Jika tanpa prisma arah awal sinar adalah arah 1 tetapi karena ada prisma arah sinar menyimpang ke arah 2.Sudut penyimpangan dinamakan sudut deviasi (δ)

Dirumuskan δ = (i1 + r2) – β
Mengapa dirumuskan demikian ?

MARI KITA BAHAS….
Perhatikan Gambar berikut.

Keterangan Gambar:

δ : sudut deviasi
β : sudut puncak prisma.(sudut pembias)
i1 : sudut datang bidang bias pertama
i2 : sudut datang bidang bias kedua.
r1 : sudut bias bidang bias pertama
r2 : sudut bias bidang bias kedua.
N: garis normal

Simbol – simbol lain, digunakan untuk membantu menjelaskan pembuktian

Langkah pembuktian pertama adalah
Perhatikan segi empat PQRS. Sudut PSR dan Sudut PQR adalah 90
β = i2 + r1 karena merupakan sudut dari garis normal (N).
Ingat , jumlah sudut dalam segi empat adalah 360 , sehingga:

< SPQ + <=”” qrs=”360″ < SPQ + 90 + 90 + < QRS = 360
< SPQ + < QRS = 360 – 180 = 180 Karena < SPQ = β ; < QRS = α maka

β + α = 180 ………….( persamaan 1)

Perhatikan segitiga SQR. Ingat jumlah sudut dalam segitiga adalah 1800 . sehingga

i2 + r1 + α = 180
α = 180 – ( i2 + r1 ) ……(persamaan 2)

Substitusikan persamaan 2, ke persamaan.1. akan diperoleh:
β + 180 – ( i2 + r1 ) = 180
β = 180 – { 180 – ( i2 + r1 )}
β = i2 + r1 ………………… terbukti !!! …………( persamaan 3)

Langkah pembuktian kedua adalah

δ = (i1 + r2) – ( i2 + r1 )

Perhatikan sudut δ, ia berpelurus dengan sudut θ, sehingga persamaan menjadi:

δ + θ = 180 ….( Pers. 4 )

Perhatikan segitiga SQδ , jumlah sudut dalamnya adalah 180 , sehingga menjadi:

λ + γ + θ = 180 ….( Pers. 5 )

dari pers 4 dan pers 5 akan diperoleh:
λ + γ + θ = δ + θ
λ + γ = δ………(Pers. 6)

Perhatikan titik S, karena sudut bertolak belakang sama besar maka:
r1 + γ = i1 atau γ = i1 – r1 ………(Pers 7)

Perhatikan titik Q, karena sudut bertolak belakang sama besar maka:
i2 + λ = r2 atau λ = r2 – i2 ………(Pers 8)

Dari (pers 6) , (pers 7) dan (pers.8) akan diperoleh:

( r2 – i2 ) + ( i1 – r1 ) = δ
atau
r2 – i2 + i1 – r1 = δ
r2 + i1 – i2 – r1 = δ

( r2 + i1 ) – ( i2 + r1 ) = δ , terbukti !! …….(Pers 9)

Subtitusikan Pers.3 ke pers 9 ,

δ = (r2 + i1 ) – β

Deviasi Minimum (m ) : sudut deviasi yang terkecil yang dapat terbentuk.
Deviasi Minimum(m ) terjadi jika r2 = i1 dan i2 = r1

Jika Hukum Snellius diterapkan pada bidang bias 1, maka

nu sin i1 = nk sin r1

nu sin ( ) = nk sin ( ) ….. mampu membuktikan????

Jika sudut puncak merupakan sudut sempit /kecil ( paralaks), maka

m = (nk – 1 ) β ….. mampu membuktikan????

nu : indeks bias udara